Paper Titles
Preface
A New Distribution and Application in Engineering Reliability
p.3
A Symbiotic Multi-Species Optimizer for Discrete Optimization
p.8
Analysis on Axial Magnetic Force of Permanent Axial Bearing by Axial Magnetized
p.12
Calculation of Leakage Coefficient for Hybrid Magnetic Bearing
p.17
Control Parameter Tuning of Magnetic Bearing PID Controller Based on Expansion Coefficient Critical Proportion
p.24
Decoupling Control for Bearingless Synchronous Reluctance Motor Based on Neural Networks Inverse
p.30
Direct Torque Control of Bearingless Synchronous Reluctance Motor
p.36
Distance Protection Application Based on Wavelet Transform and Traveling Wave Ranging
p.40

A New Distribution and Application in Engineering Reliability

Article Preview

Abstract:

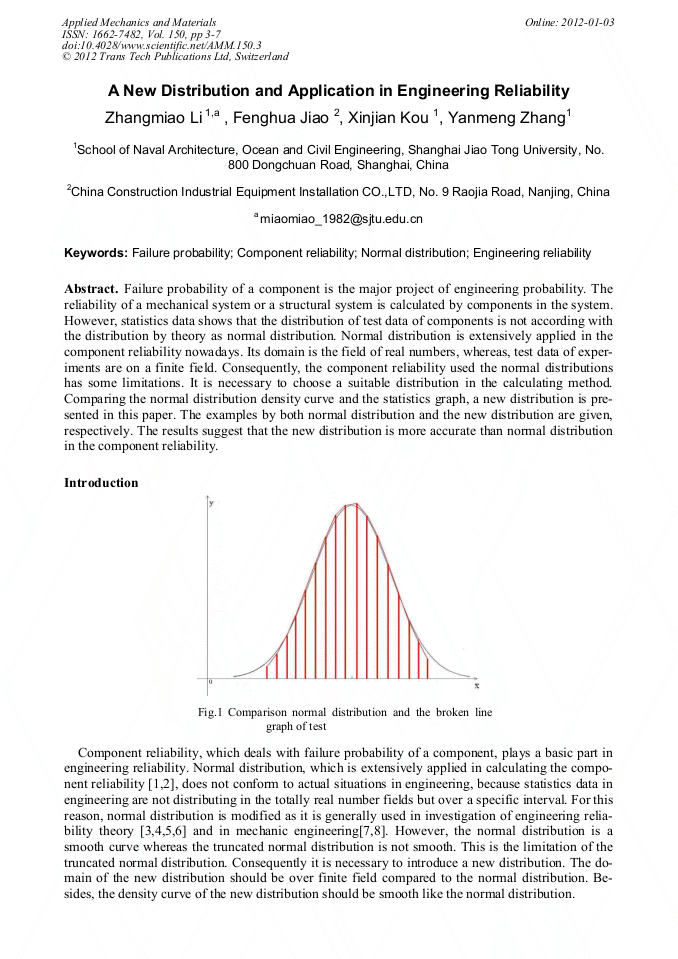
Failure probability of a component is the major project of engineering probability. The reliability of a mechanical system or a structural system is calculated by components in the system. However, statistics data shows that the distribution of test data of components is not according with the distribution by theory as normal distribution. Normal distribution is extensively applied in the component reliability nowadays. Its domain is the field of real numbers, whereas, test data of exper-iments are on a finite field. Consequently, the component reliability used the normal distributions has some limitations. It is necessary to choose a suitable distribution in the calculating method. Comparing the normal distribution density curve and the statistics graph, a new distribution is pre-sented in this paper. The examples by both normal distribution and the new distribution are given, respectively. The results suggest that the new distribution is more accurate than normal distribution in the component reliability.

You might also be interested in these eBooks
Research Progress of Magnetic Levitating Bearings and Some Advanced Technology View Preview

Info:

Periodical:

Applied Mechanics and Materials (Volume 150)

Pages:

3-7

DOI:

https://doi.org/10.4028/www.scientific.net/AMM.150.3

Citation:

Cite this paper

Online since:

January 2012

Authors:

Zhang Miao Li, Feng Hua Jiao, Xin Jian Kou, Yan Meng Zhang

Keywords:

Component Reliability, Engineering Reliability, Failure Probability, Normal Distribution

Export:

RIS, BibTeX

Price:

Permissions CCC:

Request Permissions

Permissions PLS:

Request Permissions

Сopyright:

© 2012 Trans Tech Publications Ltd. All Rights Reserved

Share:

Citation:

References

[1] O, Ditlevsen, H.O. Madsen: Structural Reliability Methods (John Wiley & Sons Ltd, Chichester 1996).

Google Scholar

[2] A.S. Nowak, K.R. Collins: Reliability of Structures (The McGraw-Hill Companies, Inc, New York 2000).

Google Scholar

[3] Michael J.A. Smith: Electronic Notes in Theoretical Computer Science, Vol. 220, Issue 3, (2008), pp.43-59.

Google Scholar

[4] Yosef S. Sherif: Reliability Engineering, Vol. 3, Issue 3, (1982), pp.209-211.

Google Scholar

[5] B.B. Pokhodzei: USSR Computational Mathematics and Mathematical Physics, Vol. 28, Issue 1, (1988), pp.91-92.

DOI: 10.1016/0041-5553(88)90223-6

Google Scholar

[6] Bradford R. Crain: Applied Mathematics and Computation, Vol. 5, Issue 2, (1979), p, 149-156.

Google Scholar

[7] Wang Dan, Zhang Yu, Zhang Fen-he and Sun Zhi-li: Mechanical science and technology, Vol. 15, No. 5(2000), pp.689-691.

Google Scholar

[8] Zhao Rui-xue, Qian Lin-fang, Chen Long-miao and Shi Hai-jun: Computer Simulation, Vol. 28, (2011), pp.248-251.

Google Scholar