Geometric Aesthetic Locus Generated by a Mechanism

Mirela Cherciu; Dan B. Marghitu; Iulian Popescu

doi:10.4028/www.scientific.net/AMM.880.81

Paper Titles

The NASGRO Method - Comparison Model for the Crack Growth Rate Calculus
p.53

Rolling with and without Slipping, during Epicycloids Generation
p.63

Rolling with and without Slipping during Orthocycloids Generation
p.69

Analysis about Influence of the Mechanical Vibrations on the Function of Shaping-Machine
p.75

Geometric Aesthetic Locus Generated by a Mechanism
p.81

Dynamic Analysis of Planetary Gear Reducer
p.87

Cam Mechanism Design for a Human Leg Exoskeleton
p.95

3D Skull Virtual Model, Based on CT or MRI Images, Used for Dentistry Simulations
p.101

Experimental Validation of an Exoskeleton for Motion Assistance
p.111

HomeApplied Mechanics and MaterialsApplied Mechanics and Materials Vol. 880Geometric Aesthetic Locus Generated by a Mechanism

Geometric Aesthetic Locus Generated by a Mechanism

Abstract:

It starts from an issue of locus that generates Rhodonea curves . It is found the equivalent mechanism, having two driving links and one dyad, RRT type, that generates series of curves with special aesthetic shapes. The process is useful in mechanical toys, at commercials where curves are generated successively on a screen, and in kinetic art. Numerous examples of curves are given.

You might also be interested in these eBooks

Achievements and Solutions in Mechanical Engineering

View Preview

Info:

Periodical:

Applied Mechanics and Materials (Volume 880)

Pages:

81-86

DOI:

https://doi.org/10.4028/www.scientific.net/AMM.880.81

Citation:

Cite this paper

Online since:

March 2018

Authors:

Mirela Cherciu*, Dan B. Marghitu, Iulian Popescu

Keywords:

Aesthetic Curves Generated by Mechanisms, Mechanisms Based on Geometric Locus of the Points

Export:

RIS, BibTeX

Price:

Permissions CCC:

Request Permissions

Permissions PLS:

Request Permissions

Сopyright:

Citation:

* - Corresponding Author

References

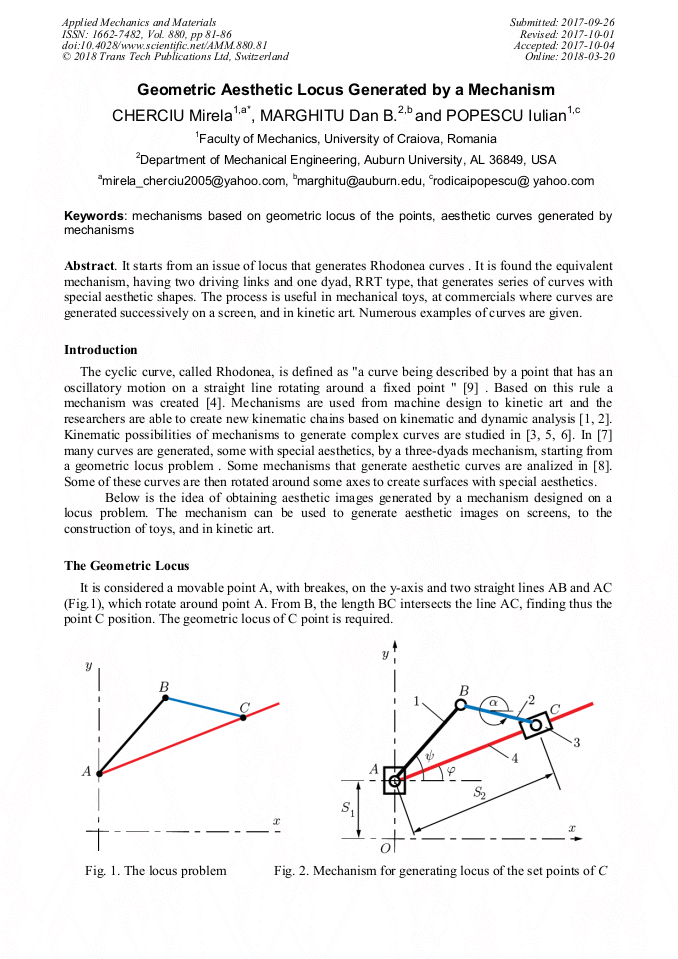
[1] Artobolevski I.I., Mechanisms in Modern Engineering Design, MIR, Moscow, (1977).

Google Scholar

[2] Erdman A.G., Sandor G. N., Mechanisms Design, Prentice-Hall, Upper Saddle River, NJ, (1984).

Google Scholar

[3] Popescu I., Mechanisms. New algorithms and programs, Reprography of the University of Craiova, (1997).

Google Scholar

[4] Popescu I., Sass L., Mechanisms for curves generating, Publishing House Scrisul Romanesc, Craiova, (2001).

Google Scholar

[5] Popescu I., Luca L., Mitsi S., Geometry, structure and kinematics of some mechanisms, Publishing House Sitech, Craiova, (2011).

Google Scholar

[6] Popescu, Iulian , Aesthetic curves and surfaces: geometry, generation, applications, Publishing House Sitech, Craiova, (2013).

Google Scholar

[7] Popescu I., Luca L., Geometric locus generated by a mechanism with three dyads, Annals of Constantin Brâncuși, University of Târgu-Jiu, Engineering Series, Issue 3/(2015).

Google Scholar

[8] Tarniţă, D., Popescu, I., Marghitu, D., Creating artistic curves with planar mechanisms, The 11th IFToMM International Symposium on Science of Mechanisms and Machines, Editor Ion Vişa, Springer Science-Business Media, 2013, pg. 233-241.

DOI: 10.1007/978-3-319-01845-4_24

Google Scholar

[9] Teodorescu, I. D., Teodorescu, Şt. D., Collection of superior geometry problems. Didactic and Pedagogical Publishing House, Bucureşti, (1975).

Google Scholar