Production of Activated Carbon from Moldy Damaged Tamarind-Pod
p.137
p.137
Biodesulfurization of Dibenzothiophene by a Newly Isolated Agrobacterium tumefaciens LSU20
p.143
p.143
A Comparison of ORC-Compress Performance with Big Data Workload on Virtualization
p.153
p.153
Investigation of Z-R Relationships for Monsoon Seasons over Southern Thailand
p.159
p.159
Ultrasonic Signal Reconstruction Using Compressed Sensing
p.165
p.165
Cross-Layer Optimization for Efficient Delivery of Scalable Video over WiMAX
p.171
p.171
A New Block Matching Algorithm for Motion Estimation
p.178
p.178
Excited-State Energy Eigenvalue Evaluation of the Quantum Mechanical Potential V(x)=½mω2x2+μx3 via Numerical Shooting Method
p.184
p.184
The Analytical Description of Projectile Motion of Cricket Ball in a Linear Resisting Medium the Storm Force
p.188
p.188
Excited-State Energy Eigenvalue Evaluation of the Quantum Mechanical Potential V(x)=½mω2x2+μx3 via Numerical Shooting Method
Abstract:
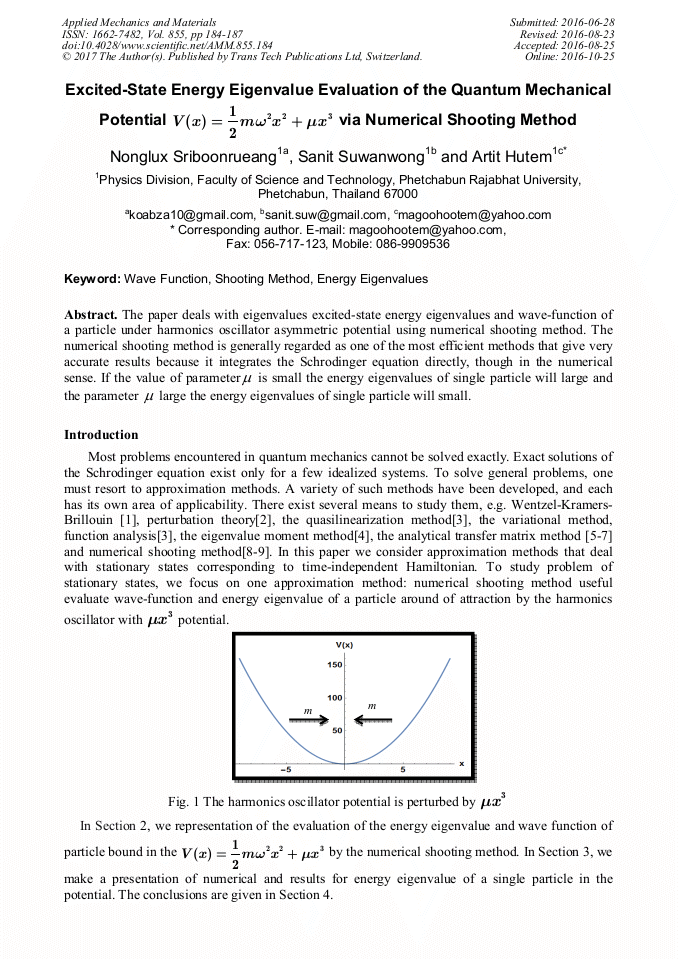
The paper deals with eigenvalues excited-state energy eigenvalues and wave-function of a particle under harmonics oscillator asymmetric potential using numerical shooting method. The numerical shooting method is generally regarded as one of the most efficient methods that give very accurate results because it integrates the Schrodinger equation directly, though in the numerical sense. If the value of parameter μ is small the energy eigenvalues of single particle will large and the parameter μ large the energy eigenvalues of single particle will small.
You have full access to the following eBook
Info:
Periodical:
Applied Mechanics and Materials (Volume 855)
Pages:
184-187
Citation:
Online since:
October 2016
Authors:
Keywords:
Permissions:
Share:
Citation: